卧式螺旋沉降离心机污泥脱水模拟研究

前言
 
卧螺沉降离心机作为一种高效的固液分离设备被广泛地应用于石油、建筑、化工等行业，利用固液两相的密度差及离心作用力来实现固体与液体的分离。在离心脱水过程中，卧螺离心机的结构参数、操作参数以及物料性质都会对脱水效果造成影响^[1-3]。由于离心分离过程的复杂性、悬浮液特性的易变性、特别是固相颗粒的形状和粒径分布的多态性，给理论和试验研究造成了极大的困难^[4]。对于物料性质来说，污泥的调质将会对后续的脱水工艺 
与设备产生较大影响，是污泥浓缩和脱水重要的前处理过程，其方法主要包括化学法、加热法、淘洗法、冷冻法和加骨粒法等，新型调质技术主要有超声、微波、热水解、磁场、电渗透、生物絮凝等^[5-7]。
 
为进一步提高脱水效果，降低污泥的含水量，G内外学者进行了大量的理论和试验研究^[8-9] 。
GRACE^[10]提出了离心机分离场中的回流现象，文献[11]提出了 Taylo-Proudman 效应，LAUDER 等^[12]
 
检验了同一型号离心机有螺旋和没有螺旋的主要区别，BATCHELOR^[13]比较详尽地建立了卧螺离心机离心分离场运动方程。大量理论和试验研究结果表明，可以从提高分离因数、增加机械挤压和延长停留时间三个方面来改善脱水性能。但试验研究因不能任意改变离心机的结构尺寸，不能同时针对多个工艺参数进行，不能系统考虑调质技术使用前后污泥脱水效率的变化而具有一定的局限性。
 
近年来，计算机技术与计算流体动力学
 
(Computational fluid dynamics，CFD)的发展为卧螺离心机流场的研究开辟了新的方向。德G学者
SCHMIDT 等^[14]应用CFD 软件考察了微米级离心分
 
离过程中结构参数的变化对离心机内部流场的影响规律。FEMNÁNDEZ 等^[15-16]应用 CFD 软件模拟了
 
工业废水在转鼓式离心机中的流动情况，模拟结果显示轴向移动的流体在气液边界面存在一个边界层，还进一步模拟了气-液-固多相流在转鼓式离心机中的流场，研究了内置径向折流板对多相流流动的影响。
 
我G化工和机械*域内的学者已利用 CFD 软件模拟了离心机转鼓内部流速与压力场的变化。黄志新等^[17]对沉降离心机圆形转鼓内流体速度进行了数值模拟，研究发现自由液面周向速率滞后随流
 
量和液池深度增大而增大，其轴向速率受流量、液池深度和转鼓转速的共同影响。郑胜飞等^[18-19]采用
 
CFD 软件以两种不同的悬浮液作为试验物料模拟了离心机的内部流场，分析了影响离心机分离的因素。于萍等^[20]对卧螺离心机离心场中固体颗粒的运动状态进行了仿真模拟，获得了转鼓转动的角速度对分离效率的影响规律。
 
本研究结合污泥调质技术对卧螺离心机进行 CFD 模拟，旨在研究卧螺离心机的长径比、螺旋及污泥黏度对分离性能的影响，同时考察不同粒径的物料在不同转速下的分离效率。
 
2 数值模拟方法
 
2.1 几何模型和网格划分
 
卧螺离心机中转鼓和螺旋输送器以一定的转差运转，以实现悬浮液的分离和沉渣的排出。模拟所用卧螺离心机的主要尺寸如下所述：转鼓圆柱段外直径 D=420 mm，圆锥段长度 L=325 mm，锥角
 
θ=8°，液层深度h=45 mm，进料管外直径D0=60 mm，进料管长度 L0=1 200 mm。
 
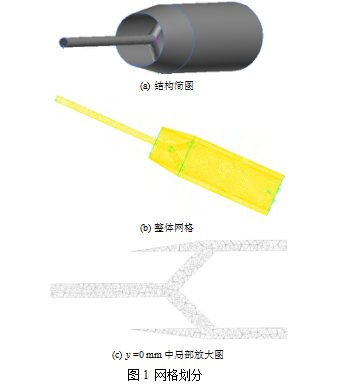
目前 Gambit 尚无法直接建立对应的几何模型，因此在模拟中shou先将各部分简化，即不考虑螺旋的作用建立三维模型，然后读入 Gambit 进行网格划分，采用 T-Grid 方法创建非结构化网格如图 1 所示，其中图 1a 为所建模型的结构简图，图 1b 所建流场整体网格划，图 1c 为 y=0 mm 处剖面的网格划分。
 
考虑螺旋的情况下，先通过 NX6.0 建立螺旋输送器的模型，用螺旋输送器切转鼓实体即可得到液
 
流区域，然后将模型转换为 CAD 图形，读入 Fluent 进行模拟计算。
2.2 边界条件和求解策略
 
计算所用液体密度为 1 015 kg/m³，液体黏度为 1.003×10^–3 Pa·s。进料管入口设为速度入口边界，指
 
定入口处的液流速度为 0.5 m/s，入口湍流强度按经验公式 I = u ¢/ u = 0.16(Re_DH )^{1/ 8} 来估算，u'为湍流脉
动速度的方均根，u 为平均速度，ReD_H  为按水力直
 
径计算得到的雷诺数，水力直径为入口管径。卧螺离心机出口为溢流出口，设定出口为 Outflow 边界条件。转鼓外壁设定为无滑移固壁边界条件，自由液面处壁面设定为滑移切应力为 0，给定卧螺离心机转鼓的转动角速度设为 30～50 rad/s，转差设置为
 
2～5 rad/s。
 
应用控制容积积分法离散控制方程组，各方程对流项的离散采用精度较高的 QUICK 差分格式，压力与速度的耦合采用 SIMPLE 算法。卧螺离心机内部流场为较为复杂的旋转占优流动，因此选取精度较高的 RSM 湍流模型封闭控制方程组。模拟固
 
体颗粒的运动过程时选取 DPM 模型，考虑螺旋输送器时选取滑移模型^[21]。
 
3 结果与分析
 
3.1 整体流场
 
选取离心机长径比为4、转鼓角速度为50 rad/s，
 



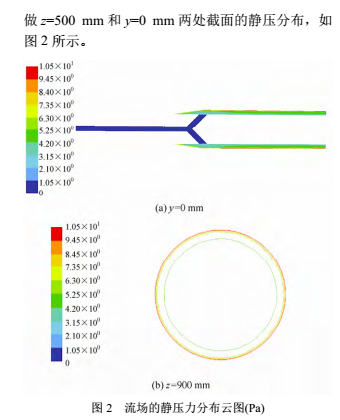
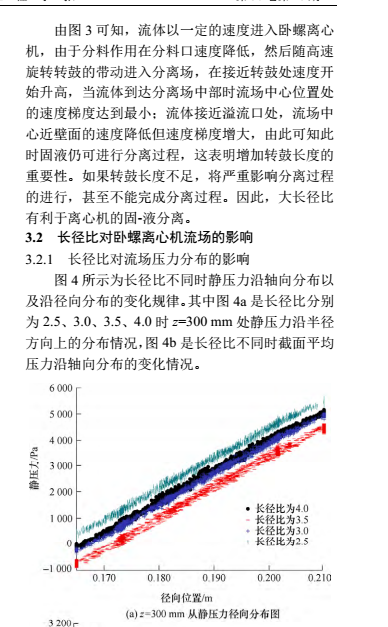
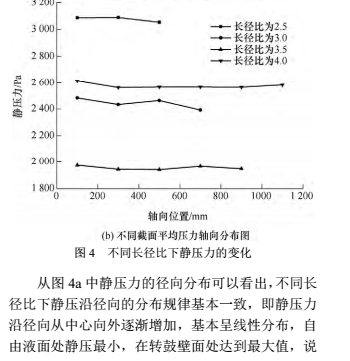
明增加液环层的厚度静压力值会显著增大。当长径比从 2.5 增大到 3.5 时，同一径向位置处的静压随着长径比的增大而减小，说明此时增大长径比可以减小阻力损失。但是进一步增大长径比，即长径比由 3.5 增大到 4.0 时，同一径向位置处的静压随着长径比的增大而迅速增大，说明此时增大长径比将增加阻力损失。从图 4b 中截面平均压力沿轴向的分布可以看出，同一长径比下截面平均压力沿轴向的变化不大，但是同一轴向位置处截面平均压力随长径比的变化较大，随长径比压力的变化与径向分布规律类似。
3.2.2 长径比对切向速度分布的影响
 
卧螺离心机转鼓内液流的流动方向可以分为轴向、切向和径向三个方向，其中轴向速度和切向速度可以表征离心机分离过程的效果。轴向速度是表征卧螺离心机生产能力的一个物理参量，轴向流速越大，表示生产能力越强，但轴向速度过大又会导致脱水效果下降，致使沉渣含湿率上升。
 
卧螺离心机的工作原理使分离液中的固体颗粒在离心力的作用下沿径向向外运动并产生分离，切向速度是分离液中固-液发生分离的关键，在研究卧螺离心机时一般采用旋转角速度进行分析。转鼓的转动带动液层一起旋转，但液体的旋转和转鼓的旋转并不一致，存在滞后现象^[17]。根据分离液基本运动方程和边界条件总结出液层任意位置处角速度与半径的关系式为

	w = w	é	æ	w¢ ö k -2				-1ù
		ê1	- ç 1-	w		÷	0	ú
	0	ê	è		0	ø	k -2	-1ú
		ë						û
式中 k0	——液面任意处的湍动能；
k	——转鼓一定转速时的**大湍动能；
ω′	——自由液面处角速度；
ω0	——转鼓角速度。

 
在液层深度为30 mm、转鼓角速度ω0=50 rad/s、入口速度为 0.5 m/s 的情况下 ω/ω0 的模拟值与计算值进行比较，如表 1 所示。
 
表 1  模拟值与计算值的比较
 

长径比	模拟值	计算值	相对误差(%)
2.5	0.630 9	0.567 3	11.21
3.0	0.631 1	0.567 3	11.25
3.5	0.630 1	0.567 3	11.07
4.0	0.630 4	0.567 3	11.12

 
从表 1 中可以看出，无论是模拟结果还是计算值都表明在液层深度、转鼓转速和入口流速不变的情况下，长径比变化对切向速度影响不大，说明长径比对切向速度滞后系数的影响不明显。然而，长径比增大会使分离空间增大，从而促进固-液分离，
 
因此增大长径比有利于提高卧螺离心机的分离性能。与静压分布的研究相结合，继续增大长径比会使阻力损失显著升高，因此选择长径比时应综合考虑分离性能和阻力损失两方面的因素。
3.3 黏度对卧螺离心机流场的影响
 
3.3.1 黏度对压力分布的影响
 
黏度变化对流场静压分布的影响如图 5 所示。在黏度分别为 1.003 mPa·s、1.143 mPa·s、1.243 mPa·s、1.423 mPa·s、1.563 mPa·s，z=500 mm
且长径比为 3.5 的条件下，静压力沿半径方向的分布图。

 
 
 
 
 
 
 
 
 
 
 
 
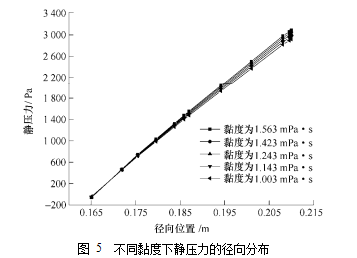
图 5  不同黏度下静压力的径向分布
 
由图 5 可知，黏度升高对自由液面附近的静压力基本没有影响，在转鼓近壁面附近静压力随黏度的升高而有一定的升高，本文考察的范围内黏度对阻力损失的影响不大。
3.3.2 黏度对切向速度分布的影响
 
因切向速度是影响分离效果的重要因素，研究不同黏度对切向速度的影响是必要的。图 6 给出了长径比为 3.5，径向坐标为 190 mm 处黏度分别为
 
1.003 mPa·s、1.143 mPa·s、1.243 mPa·s、1.423 mPa·s、1.563 mPa·s 以及 2 mPa·s 的情况下切向速度沿径向的分布情况。
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
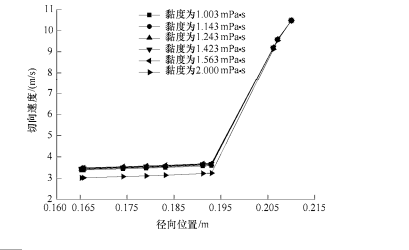
图 6  不同黏度下切向速度沿径向分布图
 
由图 6 可以看出，在黏度变化相对较小时切向速度变化也较小，随着黏度的增大切向速度逐渐降低，因此流体的黏度对切向速度有一定影响。当黏度大时切向速度相应较小，而较低的切向速度对于分离过程是不利的，因此降低流体黏度更有利于固-液分离。
3.4 污泥调质对脱水特性的影响
 
目前已有多种调质技术，使用调质技术如热水解、超声与微波等可以使污泥的特性如黏度与粒度等发生改变。下面将对有螺旋和无螺旋两种情况进行对比下，结合污泥的调质分析悬浮液黏度、颗粒的粒径分布及离心机中螺旋对分离效率的影响。
3.4.1 悬浮液黏度对脱水特性的影响
 
悬浮液的黏度主要取决于液相的黏度和悬浮液的浓度，通过理论分析和单相流场模拟可知，黏度对离心机分离效率有影响。现选取本课题组污泥
调质特性研究测得的污泥黏度作为模拟数据，分析调质技术对污泥脱水效率的影响，不同微波条件处理后的污泥黏度如表 2 所示，经过微波调质后污泥的黏度发生变化。
 
表 2  微波调质后的污泥黏度
 

	微波温度/℃	黏度/(mPa·s)
	20	12.880
	50	13.982
	60	14.836
	70	11.270
	80	12.938

 
研究中通过 DPM 模型、对不同长径比下转鼓角速度为 50 rad/s、入口速度为 0.5 m/s 时卧螺离心机内的固-液分离过程进行模拟，模拟得到的不同工况下的分离效率如表 3 所示。

		表 3			不同长径比下黏度对分离效率的影响							%
黏度/(mPa·s)	长径比为 2.5				长径比为 3.0			长径比为 3.5			长径比为 4.0
	无螺旋	有螺旋			无螺旋	有螺旋		无螺旋	有螺旋		无螺旋	有螺旋
11.270	83.33	89.63			86.44	91.04	90.14		93.41	94.91		96.45
14.836	83.23	89.23			86.35	90.13	90.07		93.78	94.87		96.27

由表 3 可以看出，在无螺旋情况下，随着黏度的增大，离心机分离效率略有降低，由于黏度变化值较小，所以分离效率的变化幅度不是很明显；相同黏度下，分离效率随着长径比的增大而增大，说明大长径比有利于固-液分离，上述结果与单相流场的模拟结果以及理论分析结果相符合。而在有螺旋情况下，随着黏度的增大离心机分离效率有增有减，这是由于黏度的变化幅度不大，而且在螺旋的作用下流场内湍流变化明显，与层流理论不相符合。但在相同黏度下，分离效率随长径比增大而增大，说明即使在有螺旋的情况下大长径比离心机也利于固-液分离。有螺旋与无螺旋这两种情况相比，由于螺旋的推进作用有促使颗粒向离心机圆锥段运动，其次螺旋还可阻挡部分回流的固体颗粒，因此离心机中的螺旋设计促进了固-液两相的有效分离。
3.4.2 粒径分布对脱水效果的影响
 
粒径分布是影响固-液分离的重要因素之一，相同体积分数下不同粒径分布的污泥其脱水效率也有所不同。为了研究固-液分离时的**佳粒径分布及离心机中螺旋对分离效率的影响，指导污泥的调质改性方向，采用 DPM 模型、滑移网格对不同粒径下固体颗粒的运动过程进行模拟仿真，从长径比为4.0、入口速度为 0.5 m/s 时各转速条件下颗粒的分离效率出发，对于悬浮液中不同的固相粒度分布得出不同的分离效率。图 7a 是无螺旋时粒径为 80 μm
 
的颗粒的运动迹线图，图 7b 是有螺旋时颗粒运动迹线图。图 7a 中颗粒的运动轨迹明显比图 7b 中稀疏，且颗粒的运动轨迹并非为规则的螺旋运动，不利于固-液的分离，而图 7b 中颗粒的运动轨迹密集及运动轨迹长且大部分做螺旋运动，可知图 7b 中颗粒在离心机中的停留时间足够长且做螺旋运动，这都有利于固-液的分离。

 
 
 
 
 
 
 
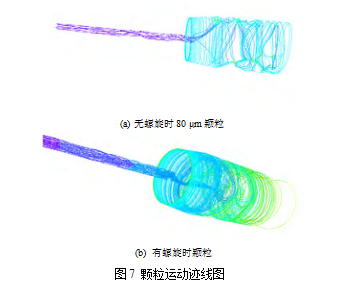
(b) 有螺旋时颗粒
 
图 7  颗粒运动迹线图
 
表 4 是转鼓各转速条件下不同粒径物料的分离效率。表 4 可以看出，随着转鼓转速的增加，分离效率随之增大，而悬浮液中颗粒粒径越大，其分离效率越高，反之越低。这是由于转速越大、颗粒粒径越大，颗粒所受离心力越大，越有利于固-液分离。 设计的机型，在降低离心机能耗的同时，也能保持根据粒径分布来选择合适的转鼓转速并选用有螺旋 卧螺离心机分离效率维持在较合理的水平。
 
 
4 结论
 
本文采用流体力学软件 FLUENT，将离心机三大基本方程与 CFD 仿真软件有效结合，分析了理论和试验中尚难以处理的结构复杂的卧螺离心机旋转流场。研究了流场速度和压力分布的变化规律，并有针对性地得到了部分操作参数对分离场的影响规律。
 
(1) 在单相无螺旋流场中，随着长径比的增大，转鼓内壁处**大压力值先变小后增大，因此就本研
 
究的研究范围来看，大长径比有利于固-液分离，但过大会使阻力损失显著升高，长径比为 3.5 为较佳选择。
 
(2) 黏度的增加不利于离心机分离效率提高，在本文考察范围内由于污泥黏度较低且变化不大对分离效果总体影响不大。相同黏度下，分离效率随长径比增大而增大，说明大长径比利于固-液分离。
 
(3) 离心机中螺旋的设计使得流场内层流理论发生变化，模拟结果表明离心机的螺旋设计使分离
 
效率明显优于无螺旋情况，因此螺旋的存在有利于固-液分离。